Scales | a music learning thing | python

Dev Zone Code
, ,
1

Hello! In an effort to learn both python and a bit of music theory, I started making thing little music toy thing in a while ago in python. Like a lot of my projects I tend to start them and get distracted. But felt like coming back to this one for a bit.

The idea is this; I wanted to tool to help me learn scales and highlight notes on a keyboard and guitar so I can easily map between them.

You can select a root note, and a scale. And it highlights those notes on a virtual fret board and a virtual keyboard.

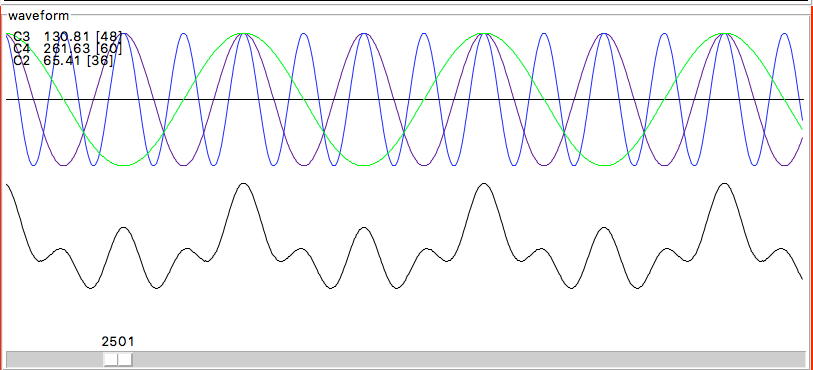
image
image818Ă—547 50.4 KB

The color coding for octaves here to make mapping notes between guitar and keyboard easier. And you can find the same chord in multiple places along the guitar.

There’s a lot of other things I want to try with it.

We can define 12 notes from A to G#. Here it is alphabetically :

notes = ('A', 'A#', 'B', 'C', 'C#', 'D', 'D#', 'E', 'F', 'F#', 'G', 'G#')

However, I prefer to start at C instead of A here because piano nomenclature & music theory is typically represented as “starting on C”. (This also makes some calculations simple as C will be used as a reference point in later calculations.)

notes = ('C', 'C#', 'D', 'D#', 'E', 'F', 'F#', 'G', 'G#', 'A', 'A#', 'B')

I chose a tuple instead of an array to keep this definition immutable / read-only.

It only supports very basic scales right now based on a triad interval and root notes:

# mode intervals
# whole/half            [w, w, h, w, w, w, h]
# tone/semi             [T, T, S, T, T, T, S]
modes = {'Ionian':      (2, 2, 1, 2, 2, 2, 1),  # major
         'Dorian':      (2, 1, 2, 2, 2, 1, 2),
         'Phrygian':    (1, 2, 2, 2, 1, 2, 2),
         'Lydian':      (2, 2, 2, 1, 2, 2, 1),
         'Mixolydian':  (2, 2, 1, 2, 2, 1, 2),  # dominant
         'Aeolian':     (2, 1, 2, 2, 1, 2, 2),  # natural minor | relative minor
         'Locrian':     (1, 2, 2, 1, 2, 2, 2)}

I plan to add other intervals when I can wrap my head around music terminology and a better way to represent them. There some more it can to and more I want to do with it but that’s the basic idea anyways.

I do my best to keep the code clean and conform to pep8 tho im no python guru.

More writeups coming for how I calculate notes and frequencies based on the 12-tone system.

5 Likes
2

image
image813Ă—370 25.7 KB

I also wanted live midi support to look at the frequencies and see the harmony of octaves or the chaos of dissonance in real time as you press keys.

potato video but you get the point. It shows the frequency of the ideal sine wave for a given midi notes and the sum of waves when multiple notes are pressed. kinda like a reverse fft

Its doesn’t makes sound, its not a synthesizer. It’s purely visual for now.

I wrote most this of this code a while ago and forgotten some bits, so I tricked chatgpt into helping me reverse engineer and document parts of this. Let me know of any errors.

There seems to be much terminology to refer to the same scale: (Western scale, 12-tone scale, 12-tet, Chromatic scale, equal-temperament).

The following calculations and formulas aim to conform to Scientific Pitch Notation (SPN) / International Pitch Notation (IPN). It adheres to these definitions and reference frequencies:

An octave number increases by 1 upon an ascension from B to C.
12 intervals: semitones per octave.
1 semitone = 100 cents. (1 semitone is subdivided into 100 cents)
Frequencies calculated using "twelfth root of two" rule: 2^(1/12)
1 cent = 2^(1/12) = 1.05946
1 octave = 1200 cents. (12 * 100). A frequency ratio of 2:1
1 Hz = 1 cycle / second.
Reference notes:
    Middle C = C4
    A4 = MIDI Note 69
    A440 = 440 Hz

A semitone is a musical interval that corresponds to the smallest step on a standard piano keyboard. It is the interval between one key and the next adjacent key on the keyboard, whether white or black. In Western music, a semitone is equal to half of a whole tone, which is the interval between two keys.

For example, the interval between the notes C and C# is a semitone, as is the interval between B and C.

On a guitar, each fret is a semitone.

Pitch of a note is typically expressed in terms of its frequency in hertz (Hz).

frequency = reference frequency * 2^(steps from reference note / intervals)

The reference frequency is the pitch of the reference note, which is typically A4 (also known as A440) with a frequency of 440 Hz. There are 12 semitones in equal temperament. A semitone has 100 cents.

1 cent = 2^(1/12)

The steps from reference note is the number of steps or intervals the note is from the reference note on the musical scale.

  • intervals = 12
  • A4 = 440.0Hz
  • A = 9

f = 440 * 2^((n-9)/12)

('C', 'C#', 'D', 'D#', 'E', 'F', 'F#', 'G', 'G#', 'A', 'A#', 'B').index('A')
 >>> 9

For example, if you want to calculate the pitch of C4 (middle C), you would use the following calculation:

pitch = 440 * (2^((0-9) / 12)) = 261.6255653005986

Frequency of C4 = 261.62 Hz. Where reference note = A440 & C = 0:

Mapping MIDI key ID’s to frequencies

Using A4 as a reference note. The MIDI note for A4 is 69. steps from reference note = (midi_note - a4_key_midi). Given MIDI note m:

f = 440 * 2^((m-69)/12)

pitch = 440 * (2^((60-69) / 12)) = 261.6255653005986

def midi_note_to_frequency(midi_note): 
    a4_freq = 440.0
    a4_key_midi = 69
    return a4_freq * math.pow(2, (midi_note - a4_key_midi) / 12)

Converting frequency to cents

A cent is a unit of measure used to describe the difference in pitch between two notes. It is equal to 1/100th of a semitone, which is the smallest interval commonly used in Western 12-tone music. For example are 100 cents between notes C4 and C#4.

To convert the frequency of a note to cents, you can use the following formula:

cents = 1200 * log2(frequency / reference frequency)

1200 = 12 notes * 100 cents. The reference frequency is a pitch that is considered to be the “zero” point for the scale, against which all other pitches are measured. For example, in equal temperament, the reference pitch is typically the note A4 (also known as A440), which has a frequency of 440 Hz.

Therefore, to calculate the number of cents for a given frequency in equal temperament, you can use the following formula:

cents = 1200 * log2(frequency / 440)

For example, if you want to calculate the number of cents for a frequency of 220 Hz (which is the pitch of A3), you would use the following calculation:

cents = 1200 * log2(220 / 440) = -1200

This means that the pitch of A3 is 1200 cents lower than the reference pitch of A4. A3 is 12 semitones, or 1 octave less than A4.

There’s no ryme or reason to why I chose the colors I did. but just for fun visual distinction between octaves and a clear way to visualize the same notes across the fretboard:

def get_color_for_octave(octave):
    # colorsys.rgb_to_hls(1, 0, 0)
    if octave == 1:
        return '#9400D3'
    elif octave == 2:
        return '#4B0082'
    elif octave == 3:
        return '#0000FF'
    elif octave == 4:
        return '#00FF00'
    elif octave == 5:
        return '#FFFF00'
    elif octave == 6:
        return '#FF0000'
    else:
        return 'black'

(todo: this should probably be a switch statement…ugly)

2 Likes
3

This is really neat. I learned to play guitar by ear and I have had a hard time remembering notes when I put it away for years and then get back to it. I was a band nerd and played all brass instruments so I know how to read actual sheet music but find guitar sheet music to require a degree in rocket surgery. lol

The fretboard inclusion is a really nice touch.

2 Likes
4

yep, same (the learn by ear part, i never played brass). i never learned to read music so tabs were always easier for me, to count 0-3-5-7. but yeah the idea here is sometimes i want to easily switch between guitar and keyboard and this tool helps me map 1-to-1

I want to add a staff for rendering classic notes on a sheet music view. And also a circle of fifths views. Kinda like this:

Apparently there are 2^11=2048 permutations. This also lets me know the other intervals and scales im missing.

A lot of the scales are the same but shifted >> eg:

'Ionian':   2, 2, 1, 2, 2, 2, 1, <
'Dorian':   >, 2, 1, 2, 2, 2, 1, 2

So I could optimize and instead of trying to define the interval pattern for every mode, only define that pattern once and play with some array shifting to knock out all variations.

The way I am rendering the strings on the fretboard I could easily support different tuning or different number of strings as my string api takes in a note and octave.

        self.draw_string('E', 4, x, self.string_spacing * 1)
        self.draw_string('B', 3, x, self.string_spacing * 2)
        self.draw_string('G', 3, x, self.string_spacing * 3)
        self.draw_string('D', 3, x, self.string_spacing * 4)
        self.draw_string('A', 2, x, self.string_spacing * 5)
        self.draw_string('E', 2, x, self.string_spacing * 6)

So I could makes some instrument presets, something like:

guitar6 = [E4, B3, G3, D3, A2, E2]
guitar6dropD = [D4, B3, G3, D3, A2, E2]
bass4 = [G2, D2, A1, E1]
base5 = [G2, D2, A1, E1, B0]

And the fretboard would render what ever string with what ever root tuning at the nut you’d like

I’m still struggle to wrap me head around sharps and flats. In code I am defining only sharps because frequency wise they are the same notes but the the fact that the number of sharps and flats changes based on mode confuses me still. It’s the same note but when is it flat and when is it sharp? eg:

A♯ = B♭
C♯ = D♭ 
D♯ = E♭
F♯ = G♭
G♯ = A♭
1 Like
5

Why not use a dictionary?

For example

color = {1: '#9400D3', 2: '#4B0082', ...}

def get_color(octave):
  if octave in color:
      return color[octave]
  else:
      return 'black'

You can also use chatgpt to check code/styles. While working on a project I had it generate code to play a scale/note to alert me of issues

3 Likes
6

The dictionary is cleaner. I suppose the question is how many octaves do i want to support color coding. It was somewhat arbitrary to start coloring at octave 1, perhaps Ill start ay 0 as this is closer to the lower end of hearing.

I could roughly divide the rainbow between octave 0 to say 10. Then either wrapping around the rainbow and repeat the color (eg octave 11 = octave 0)

Maybe go with the range of human hearing → start and end octave?
Or everything outside of human hearing could be black?

There’s lot of ways to play with how to display information. Im just making things up as i go along.

7

Another fun way to color might be by note instead of octave. divide the rainbow between 12 and each note gets that color. Or maybe a specific note should have a specific color.

I always found synesthesia fascinating; the type you could see sounds as colors. What if every time you heard a Bâ™­ you saw/felt green?

8

I would do color related to note. Then I would distinguish octave by different shades of the note. Find the standard color and start from C if you are focusing on Piano. High C would be a lighter color in comparison to low C. Or you could start with A440 if you primary focus is for guitar.

Similar color for a note will help with sight reading. Even if you hit the wrong octave, you are still on the right note so it will not sound dissonant.

1 Like
9

Probably late to this party, but looking at your Modes, I thought that it might be better to not actually list them out, so much as have a function to create them.

Then I had to work out how to write such a function that wasn’t so messy as to be pointless, which was quite interesting.

This is my code:

tone_scale = [2, 2, 1, 2, 2, 2, 1]

def selectedMode(selected):
    if selected == "Ionian":
        print(tone_scale)
    elif selected == "Dorian":
        out_scale = tone_scale[1:]
        out_scale.append(tone_scale[0])
        print(out_scale)
    elif selected == "Phrygian":
        out_scale = tone_scale[2:]
        out_scale.extend(tone_scale[:2])
        print(out_scale)
    elif selected == "Lydian":
        out_scale = tone_scale[3:]
        out_scale.extend(tone_scale[:3])
        print(out_scale)
    elif selected == "Mixolydian":
        out_scale = tone_scale[4:]
        out_scale.extend(tone_scale[:4])
        print(out_scale)
    elif selected == "Aeolian":
        out_scale = tone_scale[5:]
        out_scale.extend(tone_scale[:5])
        print(out_scale)
    elif selected == "Locrian":
        out_scale = tone_scale[6:]
        out_scale.extend(tone_scale[:6])
        print(out_scale)

selectedMode("Locrian")

Current output would be:

[1, 2, 2, 1, 2, 2, 2]

Which matches to what you have.

Obviously, this isn’t smaller than what you have - but the advantage it has is that when you come to do say - Harmonic Minor scales - you can copy paste this - change the names and the tone_scale Whole Step / Half Step - and you will get your results, and then you can repeat for any new scales you want to introduce - rather than hard coding a value.

Now in my code above, I have given these names - so that we can see what is going on - but you could just give them numbers - and a choice elsewhere dictates the number sent to the function - and that way - you could copy and paste and ONLY change the tone_scale itself for new scales - with a choice being made elsewhere in the code, and that choice dictating which function is called with which number - to get the result you wanted.

As I say, a bit late, but an interesting function to create.

Edit:

Then I go look at the code and at no point do you use the “modes” lol - still it was interesting to create and I learnt a little thing about python I hadn’t thought of before…

2 Likes
10

Not at all late. There’s no timeline on this, i mostly program for fun. Also I’m terribly scatterbrained at times, been busy IRL and other projects.
Thanks for your input!

Hmm yes, you could regenerate the outscale by shifting the array like you suggest. That’s kinda the track i was heading with generating different sets of intervals using 1 source interval set.

I’m looking for a way to generate any scale. Currently I’m using the modes for the interval definition. Meaning relative to the root note, which is the next note in our scale? Where root note is the often the lowest/first note in your chord

def generate_scale(root_note, intervals):
    """ build up a scale as defined by the root note as the starting point, and the intervals as steps """
    new_scale = []
    note = notes.index(root_note.upper())
    for x in range(len(intervals)):
        offset = intervals[x % len(intervals)]
        new_scale.append(notes[note % len(notes)])
        note += offset

    return new_scale


# create triad chord
def get_triad(root, scale):
    return [scale[(root + 0) % len(scale)],  # root | tonic
            scale[(root + 2) % len(scale)],  # third | mediant
            scale[(root + 4) % len(scale)]]  # fifth | dominant

So I need a way to generate all interval permutations. Or have a simpler / intuitive way to select your scale or make you own just selecting notes.

For example, I’m not sure listing them out as terms such as “lydian” is practical or useful. I’ve never been to a jam and heard someone say “hey lets play in dorian”. Those terms seem perhaps dated. I’m trying to wrap my head around all this music terminology.

Maybe a scale identification functions too. Where based on the selected notes, or maybe the midi input. EG: if i hold down notes C,E,G on the keyboard; auto classify that scale and those intervals → C major

11

No-one says let’s play in Lydian - because Lydian isn’t really a way to play rhythm.

It is a term that describes not only the notes in the mode (because the notes in the mode are simply the major scale moved about) - but the notes in that mode that matter in that context.

For example, playing Dorian is just playing the second position of the Major scale, but playing it in the original root place.

So if you start A Major at the 5th Fret, you start A Dorian at the 5 fret, but play the second position of the G Major scale, instead of the first position of the A Major scale.

G Major notes and A Dorian notes are exactly the same notes. So why do we give it a different name - why don’t we call it G Major?

We name it so that we know we want the “feel” of Dorian, we want to accent certain notes, because those notes will sound extra good, better than if we just played the G Major scale, as we normally do, without accenting those “special” notes.

Listing them is important, because if you just list the notes - you are just listing the major scale, you are not giving the context or flavour of that mode - that is necessary when playing modes.

And to tack on at the end - generating scales/modes might be a little more difficult simply because while the Major/Minor/Modes set are pretty simple (The Ionian and Aeolian are the major minor in any event) - once you introduce Harmonic Minor, Melodic Minor and more exotic scales - you will find that there is no interval system that works on all of them simply by moving bits around - you will have to have a separate interval system for those scales.

Which programmatically isn’t difficult, just means that there is no one-size-fits-all solution for generating scales.

1 Like
12

Hmm…

I think one of the biggest challenges for me is wrapping my head around all this music terminology. The problem has been trying to figure out how I should define a scale both musically and programmatically.

For example:

  • what makes a scale minor vs major?
  • what is a harmonic minor vs melodic minor?
  • what is the difference between a scale and a mode?

Does it even useful to just generate and list every permutation? Maybe its better to sort by “feel” how ever you define that.

I was planning to make every different interval systems for the different scales. But this may introduce another issue, I don’t want a massive drop down list of 1000’s of permutations and all this musical jargon.

I’m thinking now it might make more sense to flip around the problem; given a set of notes, can you identify the scale / mode.

Let the user select / highlight notes on the keyboard or fretboard, or from live midi input and display “you are playing an Fm7” or whatever the input happens to be.

13

I think the identification of chords based on whatever notes are played is a great idea, and very useful, if it is something you can introduce you definitely should…

There are resources online that give you all the notes of the major chords - you may find better than this - but it does the job:

Bear in mind that this should not be limited to the order shown.

C Major for example is C E G, but it is also E C G, E G C, G E C ,G C E - as these are all inversions of the C Major triad, so the 1st 3rd 5th, or the 3rd 1st 5th or the 3rd 5th 1st or the 5th 3rd 1st or 5th 1st 3rd.

  • what makes a scale minor vs major?

Well you have the intervals already, I think they are in your code. If you mean, what makes a scale sound minor? That is a bit of an anthropological question really…they just sound sad vs happy to most people, not sure why.

  • what is the difference between a scale and a mode?

In terms of the notes as absolutes, nothing at all.

As I mentioned in my post above, the same notes exist in the A Dorian mode and G Major scale - they are identical.

I cannot find a helpful way to explain this…but you can experience it, without being overly musical.

Play these notes with a count like this and loop it if you can. With Reaper or a pedal or whatever DAW you have…

1 2 3 4 5 6 7 8
A B C E G E C B

Just a walk, nothing fancy, keep a straight time, 4/4 doesn’t need to be fast. Just two bars, at 120bpm 1 2 3 4 5 6 7 8

Then play an A Minor chord over that, don’t strum it, just let it ring out, do that for a few bars, then whenever you ready, move the chord to G Major and let the chord ring out.

It feels like something has changed, not just the chords, but the notes you were playing - it feels different - but it is a loop - it didn’t change, but it feels different.

This is because there is an interplay between the notes you are playing, and the notes in the chords - this interplay is what makes modes interesting.

For instance, in the notes that you played, the C is the 3rd of the A Minor scale, which gives it a minor feel, but the C is the 4th of the G Major scale - so when you play the G Major - it has a different impact, it sounds different, the 4th has a different interaction to the 3rd in our ears.

This on a very basic level - because you need to do a little more - is essentially changing the walk we did from an A Minor scale to the A Dorian Mode, the notes that we played are the same in both (not all the notes are the same in this scale and mode) so it is the interplay that decided the feel.

  • what is a harmonic minor vs melodic minor?

Natural, Harmonic, Melodic they are all just version of the Minor scale, with different intervals.

Why, I don’t really know the answer to that to be honest, I suspect that someone at some point in time made a mistake with the minor scale and said - wow that sounds good and now we have more than one version…

1 Like
14

Not sure they will let me post an MP3 but this is actually a clip I sent to a friend about 3-years ago - who was struggling with the same modal problem as you.

He is a drummer so didn’t play any instruments - oddly, wouldn’t let me post an MP3 - understandable I suppose avoid piracy - but did allow me to render it as a WEBM and that is a file format that is accepted…

Making no bones about this playing btw, I threw this together for a friend to show him how the same notes will sound different.

1 Like
15

There are overlapping ideas about efficiency in literature. When writing music in different scales, it’s essential to use sharps and flats to avoid double flats or double sharps, ensuring efficiency similar to coding in Python. Specifically, when ascending in a melodic minor scale, sharps are used, and when descending, flats are used. This practice aims for efficiency in writing, preventing scenarios with double flats or double sharps.

1 Like