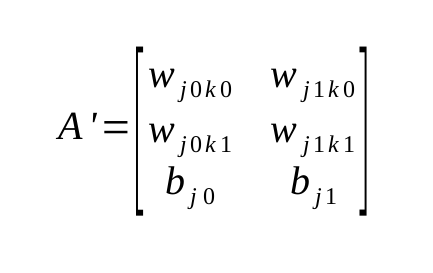Day 1
Overhauled the nums executable command line options parsing with help from an awesome go-flags package. Now i’ve got a friendly output for how to use it. Also added and implemented all of the profiling options for use later.
bin ➤ ./nums -h git:master
Usage:
nums [OPTIONS] <new | run | train>
Profiling and tracing options:
--cpuprof= Turn on CPU profiling
--trace= Turn on runtime tracing
--memprof= Turn on memory profiling
Help Options:
-h, --help Show this help message
Available commands:
new Create an empty network
run Run the network on test data
train Train on a given network.
More importantly I want to describe what I went through and how I’m planning to implement the network, to both share my thoughts/findings and review:
A neural network is basically is a graph with an input and output layers + any number of layers in between. Every node is connected to all of the following layer nodes (this is important, explain later). My first instinct, of course, was to implement it as a graph.
type Node struct {
Activation float32
Nodes []*Node
}
It became obvious early that this will never perform well:
- You cannot vectorize this
- To calculate a single node activation, you’d need to deference every connection, so you’d probably cache miss every single time, at least +100ns for every single weight. And neural networks are big, this will add up fast
So, I’ve reworked Node into an array of connections (weights), since it’s connected to every single node in the next layer, you can just keep an array.
type Node struct {
Activation float32
Weights []float32
}
This is heaps better than the last option, so I went with this. I’ve implemented the network traversal, and calculating of activations, all was well and good, I got the vectorization I wanted. Until it was time to implement backpropogation. Essentially, backpropogation is done after you calculate the activation for a training input, and then start moving backwards through the graph, taking every activation/weight/bias and making a ratio of everything while going through to the front of the network (input). This ratio tells you how much you need to adjust the values of every single weight and bias.
So what you want optimally, is for every node to have every weight that is connected to it, also in vectorizable state to allow for acceleraton. And those weights are one per each previous layer of nodes. You have to load every single one, from every single node of the previous layer. The code got convoluted fast. Not good for speed either.
So after some hours of trying to figure this out, trying to learn the math, seeing that matrices are being used in some places to explain, I figured I’d try to implement with matrices, maybe that would be easier. Computers are good at matrices right?
So I organized my matrices like so:
type LinearRegression struct {
// ...
matrices []*mat.Dense
}
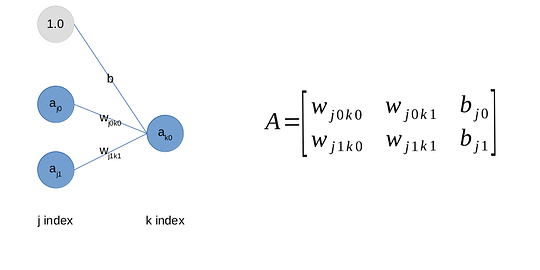
One matrix represents a layer of connections, not nodes.
Due to how the underlying data is laid out, every row of the matrix is a single node’s weights to the next layers nodes, you can get that as a raw vector (yay). You may notice that gray circle. That’s how you add biases to the matrix, you just add an activation that is 1 in the right places, then the weight essentially becomes the bias (simplified the function is
a2 = a1 * w + b, a1 being prev layer activation, so you cheat this by essentially doing
a2 = a1 * w + 1 * b) . This way bias is supplied together with the weights. This is the little trick I found from StackExchange. F-kn genius. Bias needs no special treatment.
This does not fix the layout of the data. For backpropogation, I still don’t have a vectorizable layout, the right weights are still scattered. After an hour or so of staring at it furiously, it dawned on me. You simply transpose the matrix. That’s it.
This is the transposed variant of the last one. Suddenly, the row becomes a vector of those much needed connections from every single previous node. Now I can get them. As a vector. Well, almost. Underlying layout is still wrong with the package that I’m using, I only get an interface that let’s me address the members At(x, y int) float32. Not good. But I think I can get away by copying the matrix into the right layout. So I basically end up having a transposed copy for use in that moment. Good enough.
rows, cols := n.matrices[idx].Dims()
transposed := mat.NewDense(cols, rows, nil)
transposed.Copy(n.matrices[idx].T())
Volia. transposed is now the right layout, and I only need to do this once per every layer calculation, mega savings I think. I’m yet to see how this will turn out. There’s another cool idea I have to save allocations for later. The copy won’t go anywhere though, I think.
With this, you can only have networks whose nodes connect to every other node in the next layer. You could not express it differently. So this won’t work very well for networks that use mutations and add nodes spontaneously, without any hacks.
So, the entire network is expressed as an array of matrices. One layer = one matrix num matrices = num layers - 1. They can be different sizes (for different number of nodes in layers) and work properly. This is basically where I’m at right now. Tests still fail, probably because I don’t add the cheat bias activation right yet. That’s what I’m starting to work on tomorrow. I’m done for today!
EDIT: Crappy grammar.